Đường Trung Tuyến Là Gì
Trong hình học phẳng, đặc biệt là khi học về tam giác, khái niệm **đường trung tuyến** xuất hiện rất sớm và giữ vai trò quan trọng. Đây là một trong bốn đường thẳng đặc biệt của tam giác bên cạnh đường cao, đường phân giác và đường trung trực. Tuy nhiên, rất nhiều học sinh dễ nhầm lẫn giữa các khái niệm này khi học hình học.
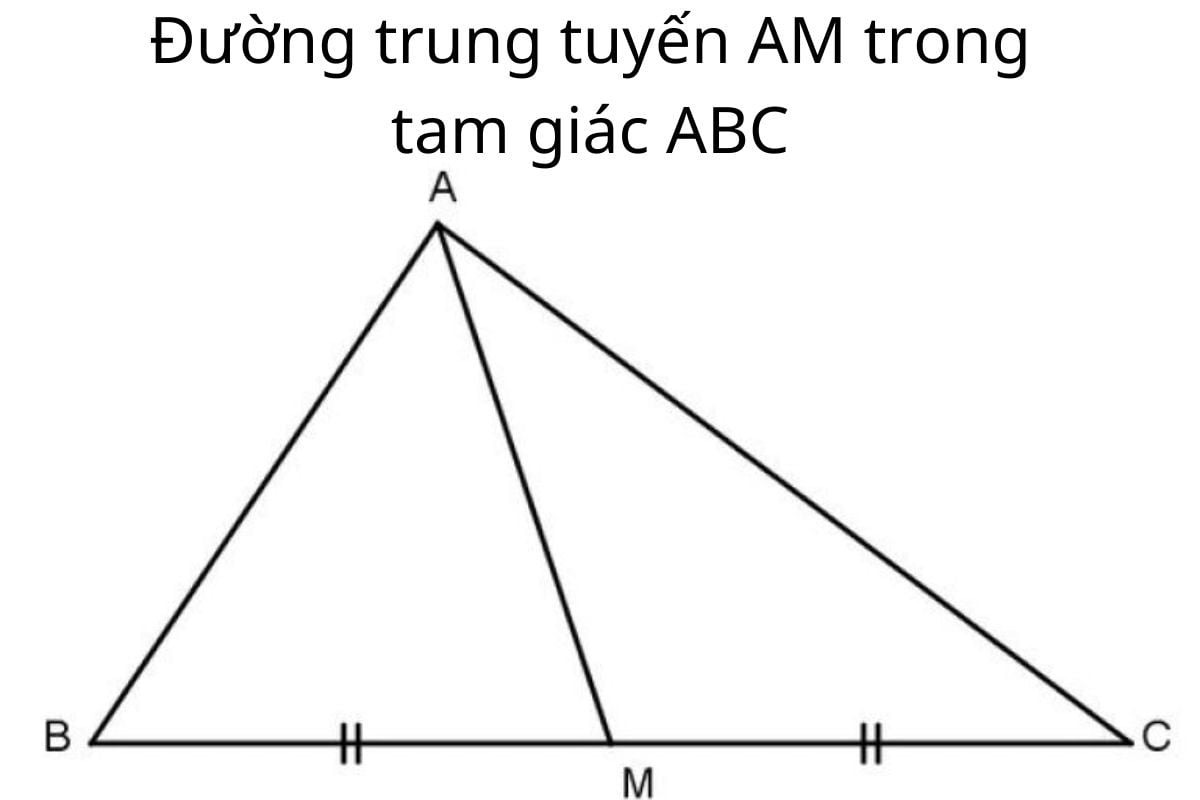
Theo định nghĩa trong sách giáo khoa, **đường trung tuyến của tam giác là đoạn thẳng nối từ một đỉnh của tam giác tới trung điểm của cạnh đối diện với đỉnh đó**. Mỗi tam giác có ba đường trung tuyến, ứng với ba đỉnh A, B, C. Những đường trung tuyến này không chỉ giúp chia cạnh đối diện thành hai phần bằng nhau mà còn là chìa khóa giúp bạn giải quyết nhiều dạng bài toán liên quan đến trọng tâm, diện tích, tọa độ trong tam giác.
Ý nghĩa thực tế của đường trung tuyến trong học tập
Khi bạn nắm rõ đường trung tuyến là gì, việc giải các bài toán về tam giác trở nên đơn giản, dễ hiểu hơn. Từ đó, bạn sẽ dễ dàng tiếp cận các khái niệm mở rộng như trọng tâm, tam giác đồng dạng, hoặc các định lý về trung điểm, tỉ lệ đoạn thẳng trong tam giác. Đây là nền tảng quan trọng cho các bạn học sinh lớp 7, lớp 8 trong hành trình chinh phục môn Toán.

Đường trung tuyến trong tam giácĐường trung tuyến không chỉ là đoạn thẳng nối đỉnh với trung điểm cạnh đối diện. Nó còn ẩn chứa nhiều tính chất thú vị, là chìa khóa để giải quyết nhanh các bài toán hình học phẳng, đặc biệt trong chương trình THCS.
Ba đường trung tuyến cắt nhau tại đâu?
Một tam giác bất kỳ luôn có ba đường trung tuyến. Ba đường trung tuyến này cùng cắt nhau tại một điểm duy nhất, điểm đó được gọi là **trọng tâm** của tam giác. Trọng tâm chính là trung điểm trọng số, giúp cân bằng tam giác trên mặt phẳng. Vị trí của trọng tâm giúp bạn dễ dàng phân chia tam giác thành các phần nhỏ có diện tích bằng nhau hoặc xác định nhanh các tọa độ trong hệ trục tọa độ Oxy.
Tỉ lệ đặc biệt khi đường trung tuyến bị trọng tâm chia đôi
Trọng tâm không chia đường trung tuyến thành hai phần bằng nhau mà theo tỉ lệ đặc biệt **2:1**. Cụ thể, đoạn nối từ đỉnh tam giác đến trọng tâm dài gấp đôi đoạn từ trọng tâm đến trung điểm cạnh đối diện. Tính chất này rất hay được sử dụng khi giải bài toán hình học liên quan đến tính độ dài đoạn thẳng hoặc bài toán về tỉ lệ.
Ảnh hưởng của đường trung tuyến trong bài toán diện tích
Một tính chất thú vị nữa là ba tam giác nhỏ được tạo thành khi nối trọng tâm với ba đỉnh tam giác lớn sẽ có diện tích bằng nhau. Đây là cách chia diện tích nhanh chóng, giúp bạn tiết kiệm thời gian khi làm bài tập về diện tích, tỉ lệ.

Hình tam giác có ba đường trung tuyến cắt nhau tại trọng tâmĐường trung tuyến không chỉ là lý thuyết mà còn mang ý nghĩa thực tế rất lớn trong các dạng bài tập từ cơ bản đến nâng cao. Từ bài toán tìm trọng tâm, chứng minh ba đường đồng quy, tính diện tích, đến tìm tọa độ trọng tâm trong hệ tọa độ, tất cả đều có sự tham gia của đường trung tuyến.
Cách tìm trọng tâm tam giác bằng đường trung tuyến
Khi cho tọa độ ba đỉnh tam giác, bạn có thể tìm trọng tâm bằng cách lấy trung bình cộng tọa độ ba đỉnh. Đây chính là nhờ mối liên hệ chặt chẽ giữa trọng tâm và đường trung tuyến. Từ trọng tâm, bạn có thể tiếp tục suy ra nhiều dữ kiện khác trong bài toán.
Vai trò quan trọng trong chứng minh hình học
Trong các bài toán chứng minh ba đường thẳng đồng quy, chứng minh trọng tâm, tìm đường trung tuyến qua trọng tâm hoặc các bài toán hình học tọa độ, trung tuyến luôn là công cụ hữu ích. Việc sử dụng chính xác các tính chất giúp bạn lập luận logic, chặt chẽ, đạt điểm tối đa trong các bài kiểm tra hay kỳ thi.
Ứng dụng để tính diện tích tam giác nhanh chóng
Biết được trọng tâm và trung tuyến giúp bạn dễ dàng chia tam giác thành ba phần có diện tích bằng nhau. Việc này rất thuận tiện khi bài yêu cầu tìm diện tích một phần tam giác, giúp tiết kiệm thời gian và tránh sai sót khi tính toán.
Ứng dụng đường trung tuyến trong giải toán hình họcĐể vận dụng hiệu quả đường trung tuyến, bạn cần biết cách nhận biết và vẽ chính xác, cũng như nắm vững những lưu ý quan trọng.
Cách nhận biết đường trung tuyến qua hình vẽ
Quan sát một tam giác bất kỳ, nếu đoạn thẳng nối từ đỉnh tới trung điểm cạnh đối diện thì đó chính là đường trung tuyến. Trung điểm cạnh có thể được ký hiệu rõ bằng dấu “tick” hoặc ký hiệu chữ cái giúp bạn dễ nhận ra hơn. Nhờ dấu hiệu này, bạn sẽ dễ dàng vận dụng các tính chất liên quan trong quá trình làm bài.
Hướng dẫn vẽ đường trung tuyến chính xác
Đầu tiên, bạn cần xác định trung điểm cạnh đối diện bằng cách dùng thước đo hoặc áp dụng công thức trung điểm nếu có tọa độ. Từ đỉnh nối thẳng đến trung điểm đó, đoạn thẳng này chính là đường trung tuyến. Khi vẽ đúng, bạn mới có thể sử dụng các tính chất liên quan một cách chính xác.
Những lưu ý khi làm bài tập liên quan đến đường trung tuyến
Đừng nhầm lẫn đường trung tuyến với đường cao, bởi đường cao luôn vuông góc với cạnh đối diện, còn đường trung tuyến chỉ nối đến trung điểm. Khi làm bài chứng minh hoặc tính toán liên quan đến trung tuyến, bạn nên kết hợp thêm các định lý như Talet, định lý trung tuyến hoặc các kiến thức liên quan để lập luận đầy đủ, chính xác.
Hiểu rõ **đường trung tuyến là gì** và các tính chất liên quan sẽ giúp bạn nắm vững nền tảng quan trọng trong học hình học phẳng. Đây không chỉ là kiến thức giúp bạn vượt qua các bài kiểm tra, kỳ thi, mà còn giúp bạn phát triển khả năng tư duy logic, quan sát hình học chính xác hơn. Từ đó, bạn dễ dàng áp dụng vào các bài toán phức tạp hơn về tọa độ, diện tích, tỷ lệ mà không còn cảm thấy khó khăn.