|
 |
 Hỗ trợ kinh doanh Hỗ trợ kinh doanh |
 |
0828 504 666 |
 |
0971 282 966 |
 |
0966 707 541 |
 |
0932 277 669 |
 baoan176pvd@gmail.com baoan176pvd@gmail.com |
|
|
|
Số Chính Phương Là Gì? Kiến Thức Cơ Bản Và Cách Nhận Biết Dễ Hiểu
18 Tháng Bảy 2025 :: 12:46 CH :: 252 Views ::
0 Comments :: BLOG
|
|
Tìm hiểu số chính phương là gì, cách nhận biết số chính phương nhanh, chính xác. Hướng dẫn nhận dạng, ghi nhớ, ứng dụng số chính phương trong học tập và giải toán hiệu quả. |
Số Chính Phương Là GìTrong toán học, **số chính phương** là một khái niệm cơ bản, xuất hiện rất sớm từ bậc Tiểu học, tiếp tục theo suốt các lớp học cao hơn. Hiểu đúng **số chính phương là gì** sẽ giúp bạn dễ dàng làm quen với nhiều dạng toán quan trọng như phân tích thừa số, giải phương trình, bất phương trình hay tìm nghiệm. Theo định nghĩa chuẩn, **số chính phương là số tự nhiên có thể viết dưới dạng bình phương của một số tự nhiên khác**. Nói cách khác, một số được gọi là chính phương khi nó bằng tích của một số tự nhiên nhân với chính nó. Ví dụ đơn giản để bạn dễ hình dung: 1, 4, 9, 16, 25, 36… đều là các số chính phương bởi chúng lần lượt bằng 1×1, 2×2, 3×3, 4×4, 5×5, 6×6. Ý nghĩa của số chính phương trong toán học
Việc hiểu rõ khái niệm số chính phương giúp bạn nhận diện nhanh khi gặp bài toán yêu cầu tìm số chính phương, chứng minh tính chất chia hết, hoặc giải các bài toán liên quan đến căn bậc hai. Đây là nền tảng giúp bạn không bị lúng túng khi bước vào các dạng toán nâng cao hơn như phương trình bậc hai, bất đẳng thức hay phân tích đa thức. 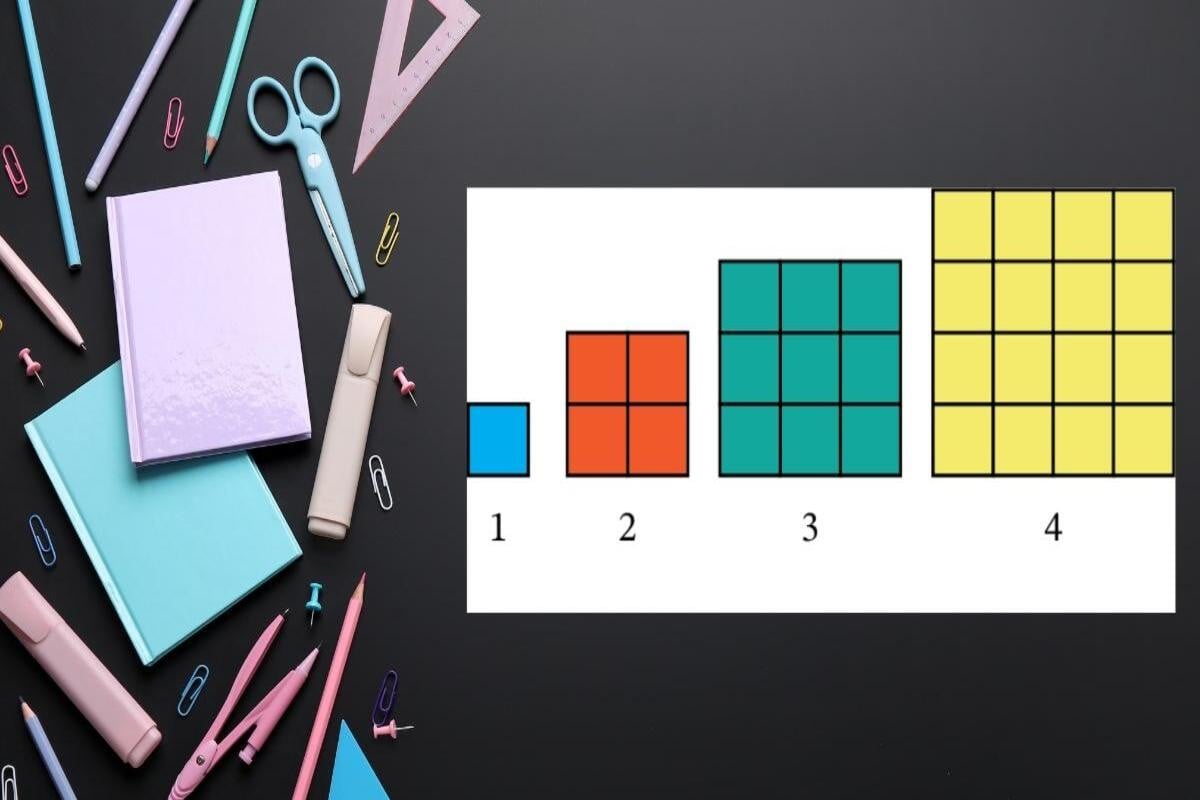
Bảng số chính phương từ 1 đến 20 giúp ghi nhớ nhanhDấu hiệu nhận biết số chính phương rất rõ ràng. Đó là các số có thể biểu diễn bằng bình phương của một số tự nhiên, và kết quả khi khai căn bậc hai của số chính phương luôn cho ra một số nguyên dương. Cách nhận biết nhanh một số chính phươngMột trong những dấu hiệu dễ nhận biết nhất là khi khai căn bậc hai, kết quả là một số nguyên dương. Ví dụ √49 = 7, nên 49 là số chính phương. Nếu căn bậc hai cho kết quả số thập phân vô hạn không tuần hoàn thì đó không phải là số chính phương. Ngoài ra, các số chính phương luôn kết thúc bằng một trong các chữ số 0, 1, 4, 5, 6, 9 (trừ số 0, các chữ số tận cùng khác sẽ không thể tạo thành số chính phương). Những lưu ý khi học về số chính phươngKhông phải số nào chia hết cho 2 hay có chữ số tận cùng 4, 6 cũng là số chính phương. Đừng nhầm lẫn giữa số chẵn, số lẻ với số chính phương. Để xác định chính xác, bạn nên nghĩ xem số đó có phải là kết quả của phép nhân một số với chính nó hay không. Ngoài ra, các số chính phương liên tiếp không bao giờ có tổng hoặc hiệu là một số nguyên tố nhỏ. Ví dụ: 4 và 9 có hiệu là 5 (là số nguyên tố), nhưng chúng không bao giờ đứng liên tiếp trong dãy số chính phương. 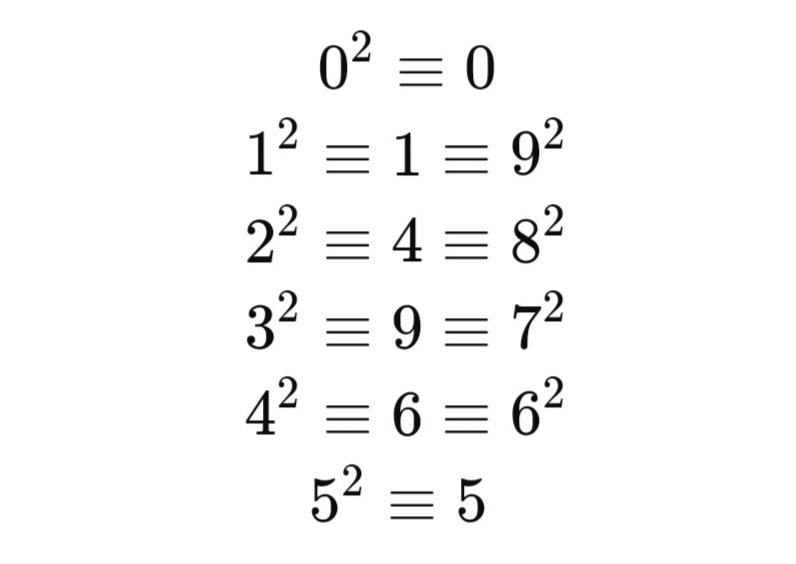
Số chính phương qua phép nhân một số với chính nóKiến thức về số chính phương không chỉ dừng lại ở khái niệm mà còn có rất nhiều ứng dụng trong các dạng toán từ cơ bản đến nâng cao. Việc nắm rõ giúp bạn dễ dàng xử lý các bài toán về số học, đại số, phương trình, bất đẳng thức… Vai trò trong bài toán căn bậc haiNhờ biết số nào là chính phương, bạn có thể khai căn bậc hai nhanh, không cần máy tính. Điều này giúp tiết kiệm thời gian khi làm các bài tập liên quan đến phương trình, biểu thức chứa căn bậc hai. Ngoài ra, khi rút gọn biểu thức chứa căn, số chính phương giúp quá trình giải trở nên đơn giản hơn rất nhiều. Ứng dụng trong các bài toán phân tích thừa sốKhi cần phân tích một số thành thừa số nguyên tố, nhận biết số chính phương giúp bạn xác định số đó có thể viết dưới dạng bình phương, từ đó dễ dàng phân tích hơn. Ngoài ra, trong các bài toán tìm bội chung, ước chung lớn nhất, hiểu rõ số chính phương cũng giúp bạn giải nhanh hơn. Tham gia vào các bài toán số học, phương trìnhSố chính phương thường xuyên xuất hiện trong các bài toán tìm nghiệm nguyên, phương trình vô tỉ, bất đẳng thức. Đặc biệt khi giải phương trình dạng x² = a, việc biết a là số chính phương giúp bạn khẳng định ngay nghiệm là số nguyên, không phải nghiệm thập phân phức tạp. 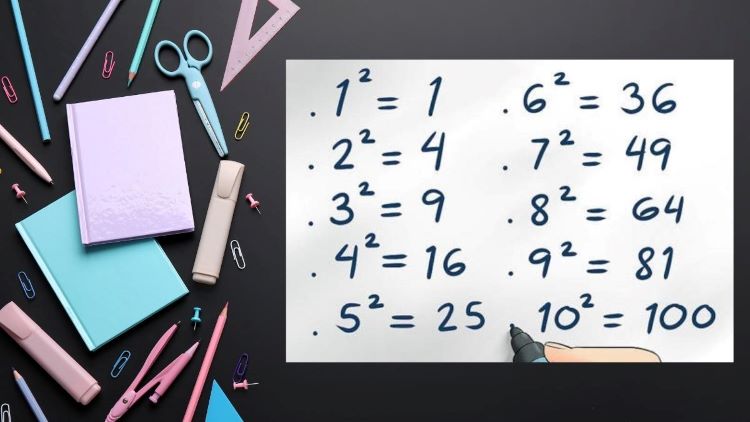
Ứng dụng số chính phương trong giải bài toán căn bậc haiĐể ghi nhớ các số chính phương một cách dễ dàng, bạn nên luyện tập bằng cách học thuộc các số bình phương từ 1 đến 20. Khi đã ghi nhớ, bạn sẽ nhanh chóng nhận diện được số nào là chính phương trong các bài toán. Học qua việc luyện tập thường xuyênViệc làm các bài tập liên quan đến khai căn, bình phương giúp bạn ghi nhớ số chính phương một cách tự nhiên, không cần học vẹt. Càng luyện tập nhiều, bạn càng quen mặt các số chính phương phổ biến như 1, 4, 9, 16, 25, 36, 49, 64, 81, 100… Nhận diện qua đặc điểm chữ số tận cùngHãy ghi nhớ rằng các số chính phương không bao giờ kết thúc bằng 2, 3, 7, 8. Điều này giúp bạn loại trừ nhanh khi làm bài trắc nghiệm hoặc nhận diện sơ bộ. Thực hành kiểm tra bằng căn bậc haiNếu phân vân một số có phải chính phương không, hãy thử khai căn bằng máy tính. Nếu kết quả là số nguyên dương, đó chính là số chính phương. Nếu là số thập phân, bạn có thể loại trừ ngay. Hiểu rõ **số chính phương là gì** và các đặc điểm liên quan là nền tảng quan trọng giúp bạn học tốt môn Toán. Đây là kiến thức cơ bản nhưng xuất hiện rất nhiều trong các dạng bài toán từ lớp nhỏ đến các kỳ thi lớn. Nắm vững, ghi nhớ và vận dụng thành thạo số chính phương sẽ giúp bạn tiết kiệm thời gian, làm bài nhanh, chính xác hơn. Hãy luyện tập thường xuyên các bài toán liên quan để khắc sâu kiến thức, đồng thời áp dụng hiệu quả trong các bài toán thực tế về số học, đại số, phương trình.>> Tham khảo: Quần áo bảo hộ công nhân
|
|
|
 |
|
|
| Comments |
Hiện tại không có lời bình nào!
|
|
Gửi lời bình
Huỷ Bỏ
|
|